El miércoles 5 de julio a las 11:00 hs. Gonzalo García Vidable defenderá su seminario:  Principios de comparación para ecuaciones parabólicas singulares en el grupo de Heisenberg, dirigido por el Dr. Pablo D. Ochoa en el Auditorio de la Facultad.

Miembros de la Mesa Examinadora: Dra. Analía Silva, Dr. Andres Aceña y Dr. Pablo Ochoa
Carrera: Licenciatura en Ciencias Básicas con orientación en Matemática
Fecha y Hora: Miércoles 5 de julio a las 11:00 hs.
Lugar: Auditorio de la FCEN

Resumen:
En la teoría de las ecuaciones diferenciales, donde la incógnita es una función definida en algún dominio y es conocido el comportamiento de cambio instantáneo local de la función -es decir, sus derivadas, en este caso parciales- la importancia de los principios de comparación radica en que pueden usarse para atacar un problema central: la unicidad
de soluciones, es decir, saber si una función o clase de funciones es la única solución posible al problema dadas ciertas condiciones iniciales.

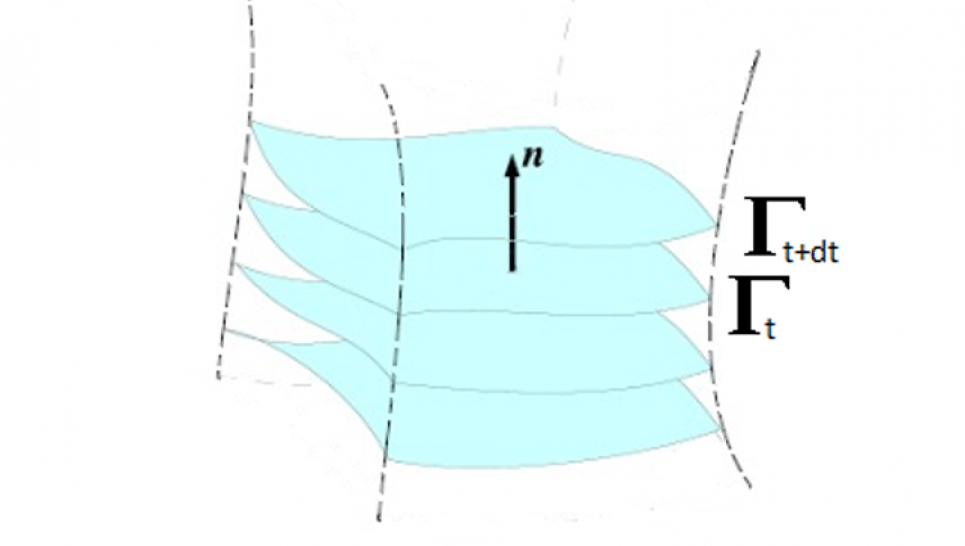
Las ecuaciones diferenciales modelan toda suerte de problemas en las ciencias aplicadas y básicas como la Física. En particular las ecuaciones parabólicas -como por ejemplo, la conocida ecuación del calor, que modela la difusión del calor en un sólido - suelen identificarse en general con problemas donde se estudia la evolución de una magnitud en una región en relación a una variable temporal. De esta clase es la ecuación de flujo de curvatura media, que describe la evolución de una superficie en el espacio y en el tiempo.

En este trabajo presentamos una demostración modificada de un Principio de Comparación conocido para esta ecuación planteada en el contexto sub-riemanniano -condición que a grandes rasgos nos dice que las direcciones de movimiento instantáneo han sido restringidas- y no abeliano del grupo de Heisenberg.